One core assumption when calculating ordinary least squares regressions is that all the random variables in the model have equal variance around the best fitting line.
Essentially, when we run an OLS, we expect that the error terms have no fan pattern.
Example of homoskedasticiy
So let’s look at an example of this assumption being satisfied. I run a simple regression to see whether there is a relationship between and media censorship and civil society repression in 178 countries in 2010.
ggplot(data_010, aes(media_censorship, civil_society_repression))
+ geom_point() + geom_smooth(method = "lm")
+ geom_text(size = 3, nudge_y = 0.1, aes(label = country))
If we run a simple regression
summary(repression_model <- lm(media_censorship ~ civil_society_repression, data = data_2010))
stargazer(repression_model, type = "text")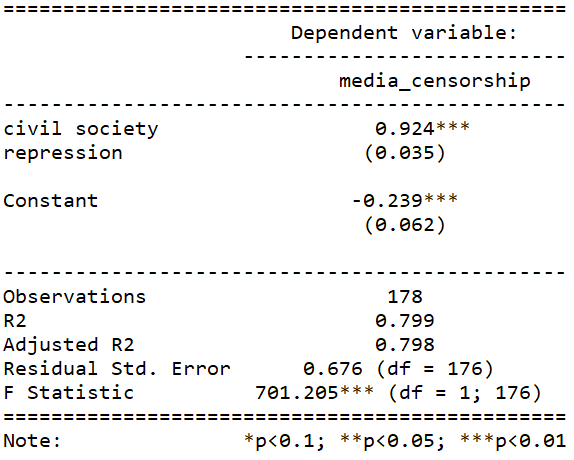
This is pretty common sense; a country that represses its citizens in one sphere is more likely to repress in other areas. In this case repressing the media correlates with repressing civil society.
We can plot the residuals of the above model with the autoplot() function from the ggfortify package.
library(ggfortify)
autoplot(repression_model)
Nothing unusual appears to jump out at us with regard to evidence for heteroskedasticity!
In the first Residuals vs Fitted plot, we can see that blue line does not drastically diverge from the dotted line (which indicates residual value = 0).
The third plot Scale-Location shows again that there is no drastic instances of heteroskedasticity. We want to see the blue line relatively horizontal. There is no clear pattern in the distribution of the residual points.
In the Residual vs. Leverage plot (plot number 4), the high leverage observation 19257 is North Korea! A usual suspect when we examine model outliers.
While it is helpful to visually see the residuals plotted out, a more objective test can help us find whether the model is indeed free from heteroskedasticity problems.
For this we need the Breusch-Pagan test for heteroskedasticity from the lmtest package.
install.packages("lmtest)
library(lmtest)
bptest(repression_model)
The default in R is the studentized Breusch-Pagan. However if you add the studentize = FALSE argument, you have the non-studentized version

The null hypothesis of the Breusch-Pagan test is that the variance in the model is homoskedastic.
With our repression_model, we cannot reject the null, so we can say with confidence that there is no major heteroskedasticity issue in our model.
The non-studentized Breusch-Pagan test makes a very big assumption that the error term is from Gaussian distribution. Since this assumption is usually hard to verify, the default bptest() in R “studentizes” the test statistic and provide asymptotically correct significance levels for distributions for error.
Why do we care about heteroskedasticity?
If our model demonstrates high level of heteroskedasticity (i.e. the random variables have non-random variation across observations), we run into problems.
Why?
- OLS uses sub-optimal estimators based on incorrect assumptions and
- The standard errors computed using these flawed least square estimators are more likely to be under-valued. Since standard errors are necessary to compute our t – statistics and arrive at our p – value, these inaccurate standard errors are a problem.
Example of heteroskedasticity
Let’s look at an example of this homoskedasticity assumption NOT being satisfied.
I run a simple regression to see whether there is a relationship between democracy score and respect for individuals’ private property rights in 178 countries in 2010.
When you are examining democracy as the main dependent variable, heteroskedasticity is a common complaint. This is because all highly democratic countries are all usually quite similar. However, when we look at autocracies, they are all quite different and seem to march to the beat of their own despotic drum. We cannot assume that the random variance across different regime types is equally likely.
First, let’s have a look at the relationship.
prop_graph <- ggplot(vdem2010, aes(v2xcl_prpty, v2x_api))
+ geom_point(size = 3, aes(color = factor(regime_type)))
+ geom_smooth(method = "lm")
prop_graph + scale_colour_manual(values = c("#D55E00", "#E69F00", "#009E73", "#56B4E9"))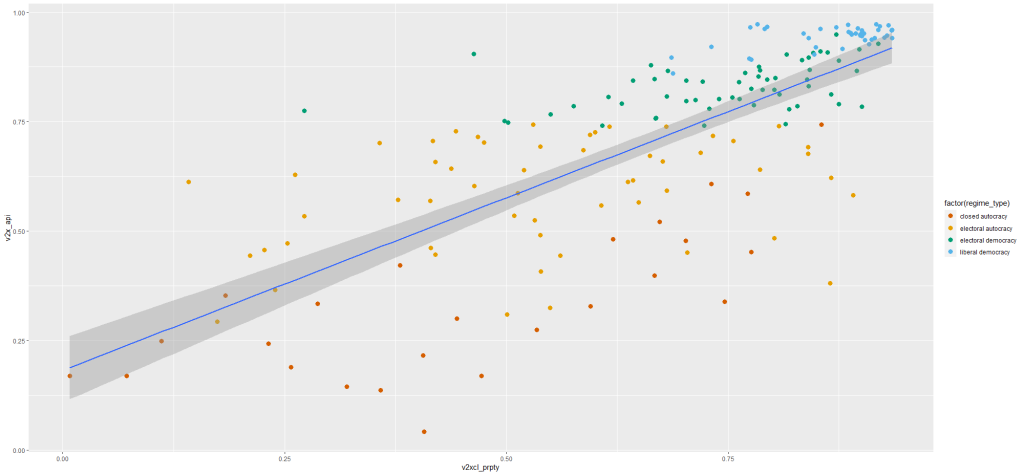
Next, let’s fit the model to examine the relationship.
summary(property_model <- lm(property_score ~ democracy_score, data = data_2010)) stargazer(property_model, type = "text")

To plot the residuals (and other diagnostic graphs) of the model, we can use the autoplot() function to look at the relationship in the model graphically.
autoplot(property_model)

Graph number 1 plots the residuals against the fitted model and we can see that lower values on the x – axis (fitted values) correspond with greater spread on the y – axis. Lower democracy scores relate to greater error on property rights index scores. Plus the blue line does not lie horizontal and near the dotted line. It appears we have non-random error patterns.
Examining the Scale – Location graph (number 3), we can see that the graph is not horizontal.
Again, interpreting the graph can be an imprecise art. So a more objective approach may be to run the bptest().
bptest(property_model)

Since the p – value is far smaller than 0.05, we can reject the null of homoskedasticity.
Rather, we have evidence that our model suffers from heteroskedasticity. The standard errors in the regression appear smaller than they actually are in reality. This inflates our t – statistic and we cannot trust our p – value.
In the next blog post, we can look at ways to rectify this violation of homoskedasticity and to ensure that our regression output has more accurate standard errors and therefore more accurate p – values.
Click here to use the sandwich package to fix heteroskedasticity in the OLS regression.
Hello
I would be very cautious about using hypothesis tests to ask whether, for example, residuals are normally distributed or are homoskedastic. Firstly, the important question is not “is the distribution of my residuals significantly different from assumption X”, but “is the distribution of residuals sufficiently different from assumption X that I have to worry about my model fit”. These two things are not the same.
One way to look at this is to think about how the probability of a significant result from your Breusch-Pagan test or whatever changes as your sample size increases. With a small sample size your test will have low power and you’ll be unlikely to detect heteroskedasticity, even if it is present to a degree that will affect your model fit. With a large sample size your test has higher power, and you are likely to detect heteroskedasticity even if it is not of a magnitude that is going to affect the model fit in a meaningful way. Given that no set of residuals is ever perfectly normally distributed, or perfectly homoskedastic, then with very large sample sizes you will always detect violations of your linear model assumptions if you use these hypothesis tests, even when the magnitude of the violation is trivial. Furthermore, since linear models are generally quite robust to violations of these assumptions, particularly when sample sizes are large, you are more likely to detect apparent problems in the circumstances when these will have the least effect.
In summary then, if you don’t get a significant result on your Breusch-Pagan test it doesn’t mean that there isn’t a problem with heteroskedasticity, and if you do get a significant result it doesn’t mean that there is a problem. Overall I think most people would recommend using the diagnostic plots and thinking carefully about any patterns which are visible, and whether they are likely to be affecting the important conclusions from your model fitting exercise — do you just want to know if there’s a positive relationship or are you doing predictive work and need to know the slope of the relationship as precisely as possible? In the latter case you’ll need to be more careful than in the former.
Hope this is helpful and not too stats-splainy…
Rob Knell
LikeLiked by 2 people
Really appreciate your comment and your insights!!!
LikeLiked by 1 person
The package is ggfortify, not ggplotify
LikeLike